「月光科学」の連載をしていると、とにかく月が気になります。
昨日の夕刻、月が出ていましたのでラプトル50にEosX2を付けて
写してみました。
どうも納得の行かない写り・・・
今ひとつ改善が必要なようです・・・
さて、「月光科学」の続きです。
満月の明るさは 0.25 lx ですと昨日お話したのですが、これには条件があります。
この 0.25 lx というのは満月が頭の真上にあって、地面を垂直に照らす状態で、
なおかつ大気による減光の影響がないものとしたときの明るさです。
こういう状況の明るさを専門用語で「直射法線照度」といいます。
当然のことですが、斜めから光が差し込めば明るさは落ちますし、大気の中を
長く通ることになるので、大気の減光の影響を強く受けることになります。
斜めから光が差し込むと、どのくらい明るさが落ちるかを示す公式としては
照明計算の基礎の基礎ともいえる「余弦(コサイン)の法則」が当てはまります。
E = E0・cosθ (lx)
ここで E :θ方向から差し込んだ光による照度
E0:直射法線照度
θ:法線(真上)からどれだけ離れているかの角度
こんな風に数式になると、いきなり難しくなってしまうような気がします。
スタパおかみなどは「思考が停止するから、やめれ~ッ!」と騒ぎます。
でも冷静に考えて頂くとそれほど難しい話ではないのです・・・
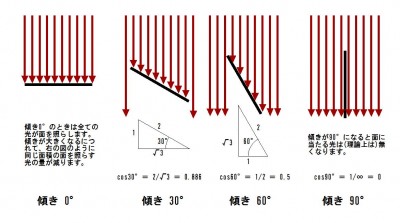
上の図で一番左は照らされる面(被照面)に垂直に光が差し込んでいる状態で、
これが基本の状態で100%の明るさです。
一番右の図は光が真横から照らされる状態で、理論的には被照面に光が
当たらないので、0%の明るさになります。
さて、ここまでは誰が考えても当たり前の話ですよね・・・
で、問題はこの真正面と真横の中間の明るさがどのように変化するか?です。
被照面が斜めになれば、見かけの面積が少しずつ小さくなるのは何となく
分かると思います。
被照面の奥行きが一定だと考えれば、面積の比は直角三角形の底辺と斜辺の
長さの比と同じです。
つまり、傾きが30°のときは 三角形の斜辺の長さを2とすると、底辺の長さは
√3(=1.732)ですから √3/2 ≒ 0.866 というのが光を受けることのできる
投影面積ということになります。
傾きが30°のときには真上から光が照射されるときよりも0.86倍の明るさに
なります。
同様に傾きが60°のときは、斜辺の長さが2とすると底辺の長さは1に
なりますから、明るさは2分の1になるというわけです。
ここで斜辺と底辺が挟む角度をθとすると
底辺 ÷ 斜辺 = cosθ
という三角関数の式が成り立つので、「余弦の法則」などと難しい言葉を
使ってひと言で済ませています。
でも、とにかく難しく考えずに、
上の図のように考えて、30°の傾きのときは1.5本ぐらい光がはみ出している。
60°のときは5本ぐらいの光がはみ出している・・・。
というふうに考えて頂ければ、斜めから光が入れば角度に応じて暗くなる
ということが理解できると思います。
ふ~っ・・・ 理系でない方にはあまり楽しくない話ですみません・・・
月の話からずいぶん離れてしまったように思うかも知れないのですが、
月が照らす角度によって地面の明るさが変わるということを知って頂き
たいわけです。
どんな天体も、地上から見ると真南に来たときに一番高く昇ります。
この時の地平線からの角度を南中高度といいますが、月の場合は
太陽と同じで、夏と冬で全く高さが違います。
太陽は夏に高く昇り、冬には低い位置までしか昇りません。
それでは月は夏と冬、どちらが高く昇るのでしょうか?
これ、次回までの宿題とさせていただきます。
ご存じない方でも冷静に考えればすぐに分かると思いますので、
ぜひ考えてみて下さい!
続く・・・